跳到主要内容

解析 Rough.js 图形线填充实现：扫描线算法

· 阅读需 10 分钟
不如怀念
不如怀念
Web 前端工程师 (Web Front-end Engineer)

最后更新于 2024-06-16 19:11:00

由于比较好奇 Rough.js 的手绘风格是如何实现的，遂准备看看其源码实现，在这个过程中发现了一个依赖项包 hachure-fill，类似铅笔线的图形填充依赖此包实现，其源码比较简洁，从其实现中了解到一个计算机图形学领域的概念-“扫描线算法（Scanline Algorithm）”。

Rough.js sample

如上图所示，在一个图形中用线进行填充，而不是某种颜色，为了实现该效果，需要基于该图形计算多条填充线段的坐标数据。

源码分析​

首先，从 hachure-fill 简洁的源代码（v0.5.2）实现来进行分析其实现思路。

该库提供了以下 API：

hachureFill(points: Point[], angle: number, gap: number): Line[]

为了计算图形内的填充线数据，需要提供该图形的顶点数据 points，同时提供了视觉效果多样化的自定义配置，允许配置填充线的倾斜角度 angle 和间隔距离 gap。

https://github.com/pshihn/hachure-fill/blob/master/src/hachure.ts#L41
export function hachureLines(polygons: Polygon | Polygon[], hachureGap: number, hachureAngle: number, hachureStepOffset = 1): Line[] {
  const angle = hachureAngle;
  const gap = Math.max(hachureGap, 0.1);
  const polygonList = (polygons[0] && polygons[0][0] && (typeof polygons[0][0] === 'number')) ? [polygons as Polygon] : polygons as Polygon[];

  const rotationCenter: Point = [0, 0];
  if (angle) {
    for (const polygon of polygonList) {
      rotatePoints(polygon, rotationCenter, angle);
    }
  }
  const lines = straightHachureLines(polygonList, gap, hachureStepOffset);
  if (angle) {
    for (const polygon of polygonList) {
      rotatePoints(polygon, rotationCenter, -angle);
    }
    rotateLines(lines, rotationCenter, -angle);
  }
  return lines;
}

根据源码中 hachureLines() 函数的实现逻辑，其首先对目标图形顶点的数据进行了旋转操作，然后调用 straightHachureLines() 函数计算得到了多条填充线的数据，最后同时将目标图形的顶点和填充线数据又做了同样角度的逆旋转操作。（为什么要做旋转和逆旋转操作后面会进行解释）

至此，我们可以先直接来看看 straightHachureLines() 函数的实现逻辑。

https://github.com/pshihn/hachure-fill/blob/master/src/hachure.ts#L62
function straightHachureLines(polygons: Polygon[], gap: number, hachureStepOffset: number): Line[] {
  const vertexArray: Point[][] = [];
  for (const polygon of polygons) {
    const vertices = [...polygon];
    if (!areSamePoints(vertices[0], vertices[vertices.length - 1])) {
      vertices.push([vertices[0][0], vertices[0][1]]);
    }
    if (vertices.length > 2) {
      vertexArray.push(vertices);
    }
  }

  const lines: Line[] = [];

  // ...

  return lines;
}

该函数首先对目标图形的顶点数据进行了简单的预处理，将所有多边形的顶点数组提取到 vertexArray 中，并确保每个多边形的第一个和最后一个点相同。这样做的原因大概基于两方面考虑：

  • 一是确保多边形闭合，如果第一个点和最后一个点不同，那么在后续处理边的时候，就会将最后一条边漏掉，导致结果不完整；
  • 二是处理自相交多边形，自相交多边形是指多边形的边相互交叉的情况，对于这种情况，单个多边形实际上被分割成了多个子多边形，算法可以将自相交多边形视为多个独立的子多边形来处理，从而正确地生成内部线条。

接下来则是填充线的完整计算逻辑实现。

https://github.com/pshihn/hachure-fill/blob/master/src/hachure.ts#L62
function straightHachureLines(polygons: Polygon[], gap: number, hachureStepOffset: number): Line[] {
  // ...

  const lines: Line[] = [];
  gap = Math.max(gap, 0.1);

  // Create sorted edges table
  const edges: EdgeEntry[] = [];

  for (const vertices of vertexArray) {
    for (let i = 0; i < vertices.length - 1; i++) {
      const p1 = vertices[i];
      const p2 = vertices[i + 1];
      if (p1[1] !== p2[1]) {
        const ymin = Math.min(p1[1], p2[1]);
        edges.push({
          ymin,
          ymax: Math.max(p1[1], p2[1]),
          x: ymin === p1[1] ? p1[0] : p2[0],
          islope: (p2[0] - p1[0]) / (p2[1] - p1[1]),
        });
      }
    }
  }


  edges.sort((e1, e2) => {
    if (e1.ymin < e2.ymin) {
      return -1;
    }
    if (e1.ymin > e2.ymin) {
      return 1;
    }
    if (e1.x < e2.x) {
      return -1;
    }
    if (e1.x > e2.x) {
      return 1;
    }
    if (e1.ymax === e2.ymax) {
      return 0;
    }
    return (e1.ymax - e2.ymax) / Math.abs((e1.ymax - e2.ymax));
  });
  if (!edges.length) {
    return lines;
  }

  // Start scanning
  let activeEdges: ActiveEdgeEntry[] = [];
  let y = edges[0].ymin;
  let iteration = 0;
  while (activeEdges.length || edges.length) {
    if (edges.length) {
      let ix = -1;
      for (let i = 0; i < edges.length; i++) {
        if (edges[i].ymin > y) {
          break;
        }
        ix = i;
      }
      const removed = edges.splice(0, ix + 1);
      removed.forEach((edge) => {
        activeEdges.push({ s: y, edge });
      });
    }
    activeEdges = activeEdges.filter((ae) => {
      if (ae.edge.ymax <= y) {
        return false;
      }
      return true;
    });
    activeEdges.sort((ae1, ae2) => {
      if (ae1.edge.x === ae2.edge.x) {
        return 0;
      }
      return (ae1.edge.x - ae2.edge.x) / Math.abs((ae1.edge.x - ae2.edge.x));
    });

    // fill between the edges
    if ((hachureStepOffset !== 1) || (iteration % gap === 0)) {
      if (activeEdges.length > 1) {
        for (let i = 0; i < activeEdges.length; i = i + 2) {
          const nexti = i + 1;
          if (nexti >= activeEdges.length) {
            break;
          }
          const ce = activeEdges[i].edge;
          const ne = activeEdges[nexti].edge;
          lines.push([
            [Math.round(ce.x), y],
            [Math.round(ne.x), y],
          ]);
        }
      }
    }
    y += hachureStepOffset;
    activeEdges.forEach((ae) => {
      ae.edge.x = ae.edge.x + (hachureStepOffset * ae.edge.islope);
    });
    iteration++;
  }
  return lines;
}

根据以上源码来看，其大致分为几步：

  1. 将顶点数据转换为多条边数据 edges；
  2. 然后对边进行排序（根据最小 y 坐标）；
  3. 然后从最小的 y 坐标开始向上迭代计算填充线（这个过程中每次迭代都会收集与当前 y 坐标相关的边 activeEdges，同时对其进行排序（按 x 坐标），计算当前 y 坐标水平线与两条边的交点即作为填充线数据）。

这里需要注意的是，每次迭代时，活动边 activeEdges 的 x 都会重新赋值一次，利用等比例缩放的原理根据 y 的步进计算得到 x 的步进。

实际上到这里，查询其它相关资料可以了解到，上述步骤是计算机图形学中 “扫描线算法（Scan-line Algorithm）” 的大致思路。

扫描线算法​

根据维基百科，扫描线算法实际上是一种图形渲染技术，一开始其作为一种高效的图形渲染技术而出现，后被应用到多个不同场景，例如我们这里所说的图形的线填充场景。

该算法的工作原理可以描述为以下几个关键步骤：

  1. 初始化多边形的边数据表（Edge Table，其中需要计算出每条边的纵坐标极值，横坐标起始点以及斜率倒数 4 个关键值）；
  2. 创建活跃边表（Active Edge Table, AET，存储当前扫描线与哪些边相交）；
  3. 以所有边中最小的纵坐标初始化扫描线 y=ymin，开始向上迭代 y；
  4. 更新活跃边表（收集与当前扫面线相交的所有边）；
  5. 根据横坐标 x 对活跃边表中的边进行排序，以确定交点的顺序；
  6. 填充多边形，在活跃边表中的边按 x 坐标成对出现，每对之间的区域为多边形内部，绘制水平线进行填充；
  7. 根据边的斜率倒数更新活跃边表中边的 x 坐标，为下一行扫描做准备；
  8. 重复步骤 4-8 直至所有边被迭代完成。

Scan-line_algorithm

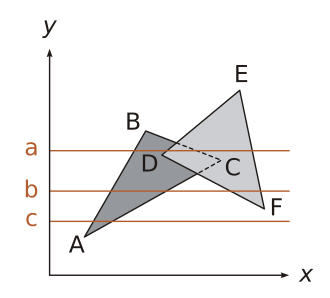
如上图所示，纵坐标最小值为 A 点 y 值，从该位置依次向上迭代计算多条平行线（即 c、b、a 顺序），并在平行线的所有像素点处进行填充。

扫描线算法原理比较简单，可查看该文章中的动画示例来更好的理解其过程。另外，该算法实现时要注意一些特殊情况，例如与扫描线平行的边需要忽略掉。

至此，可以解释为何一开始要执行图形顶点数据的旋转和逆旋转操作了，这是为了实现任意角度的填充线，因为经过旋转后在新的坐标系中可以利用扫描线算法进行迭代得到所有的水平填充线，再经过逆旋转操作可以将坐标系恢复最终得到预期角度的填充线数据。

参考资料​